堆结构基础

堆的概念与特征

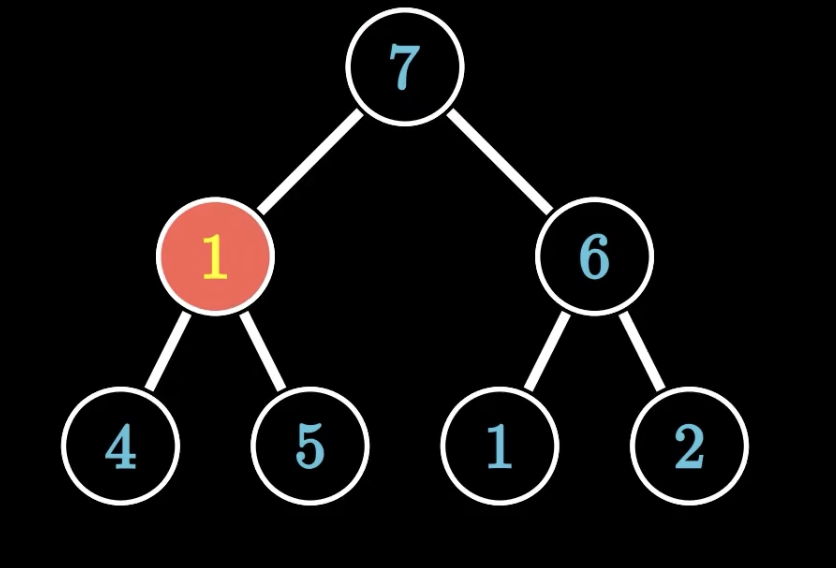
堆是将一组数据按照完全二叉树的存储顺序，将数据存储在一个一维数组中的结构。堆有两种结构：

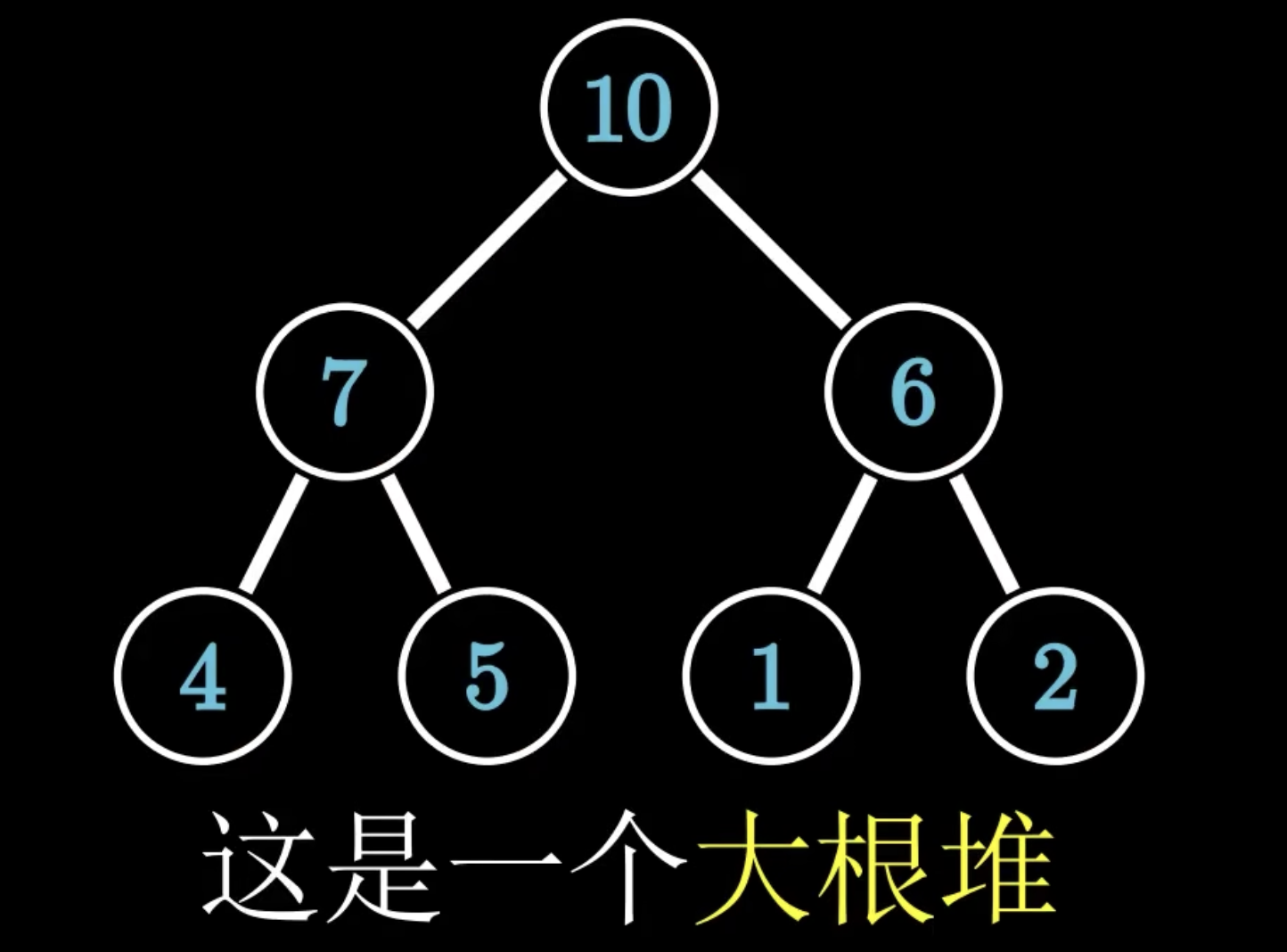
  1. 大根堆（大顶堆）：任意节点的值均大于等于它的左右孩子，并且最大的值位于堆顶，即根节点处。有些地方也叫大根堆或者最大堆，都是一个意思
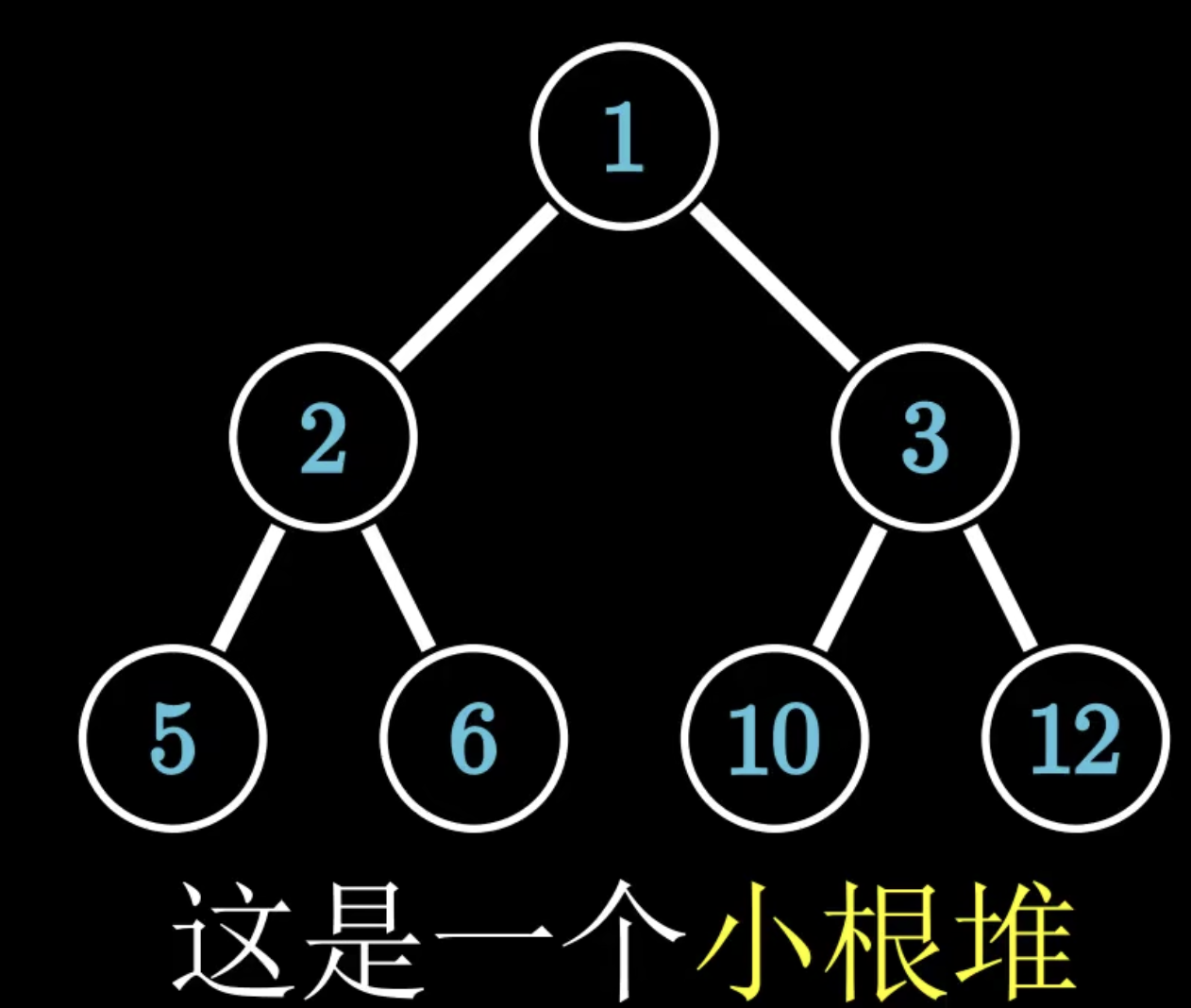
  2. 小根堆（小顶堆）：任意节点的值均小于它的左右孩子，并且最小的值位于堆顶，即根节点处。

image.pngimage.png

大和小的特征等都是类似的，只是比较的时候是按照大还是小来定

既然是将一组数据按照树的结构存储在一维数组中，而且还是完全二叉树，那么父子之间关系的建立就很重要了。
有个概念需要着重注意⚠️，我们在做题时经常会看到有些地方叫堆，有些地方叫优先级队列，那么两者的关系是什么呢？
:::info
优先级队列：说到底还是一种队列，他的工作就是 poll() / peek()出队列中最大/最小的那个元素，所以叫带有优先级的队列。能够实现优先功能的策略不一定只有堆，例如二项堆，平衡树、弦断树、C++里会用二进制分组的vertor来实现一个优先队列。
:::

堆：堆是一个很大的概念，他并不一定是完全二叉树。我们之前用完全二叉树是因为这个很容易被数组存储，但是除了这种二叉堆之外，我们还有二项堆、斐波那契堆、这种堆就不属于二叉树。

简单总结：因此，堆是一种数据结构，用来实现优先队列的一种方式。优先队列可以使用其他数据结构来实现，但堆是最常见的选择之一，因为它能够以较低的时间复杂度提供插入和删除操作。

堆的存储

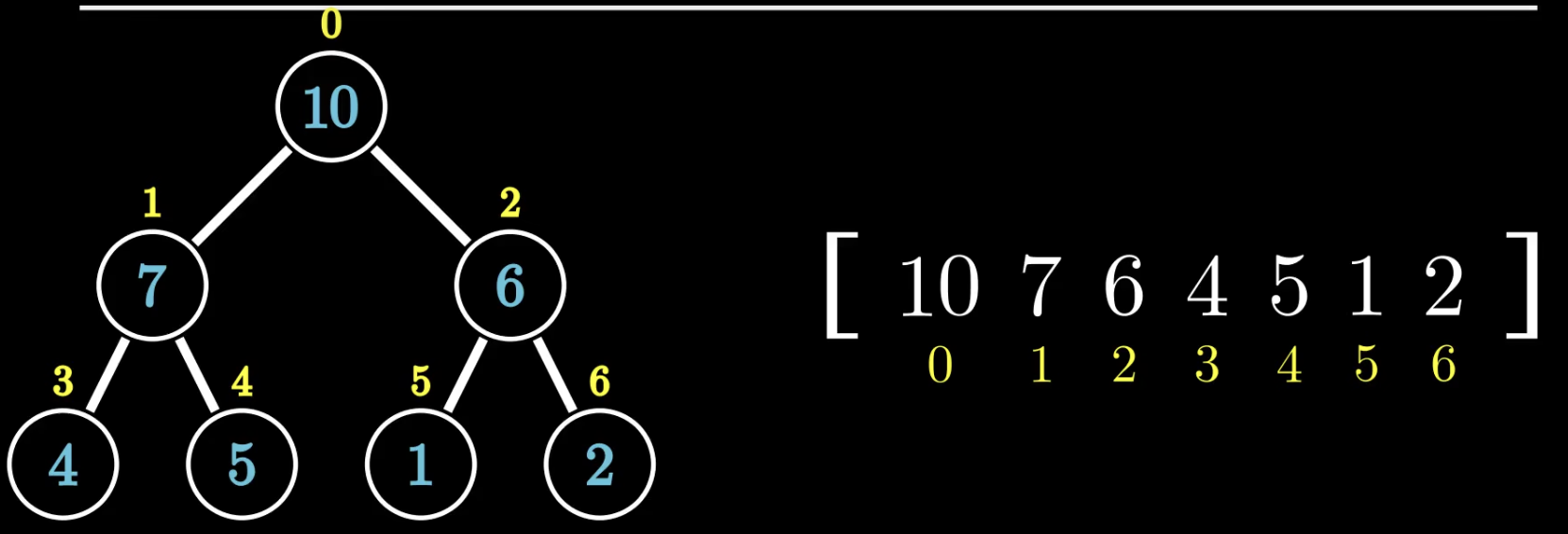
就如我们之前说的，堆是将一组数据按照完全二叉树的存储顺序，将数据存储在一个一维数组中的结构。
我们按照层序遍历的方式存储，这样数组的下标和树是一一对应的！
image.png
节点下标的规律为：
这个计算方式会被经常用到，所以请背过！！！
image.png

堆的基本操作

堆的基本操作分为两种：

上滤

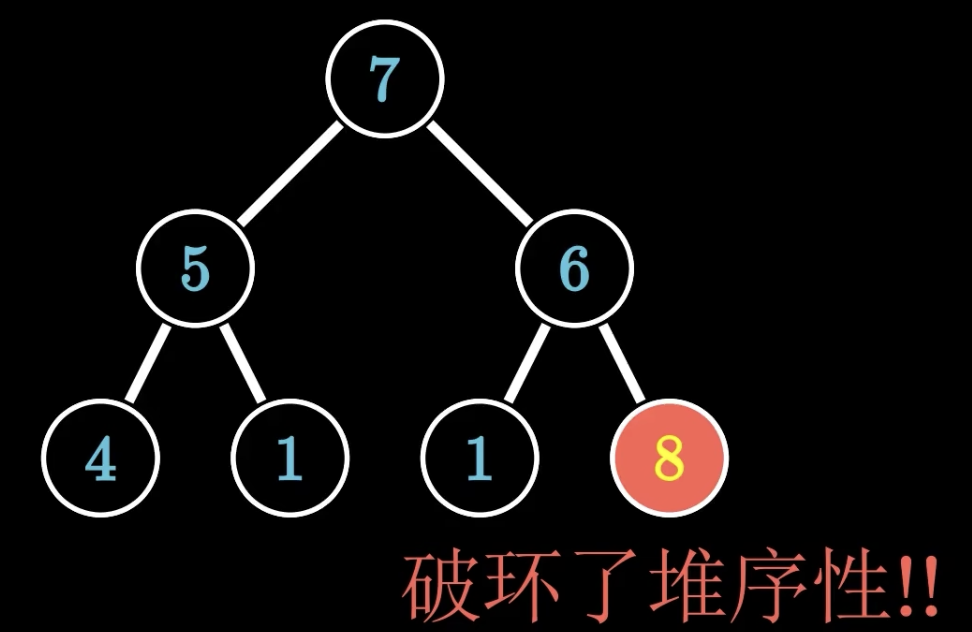
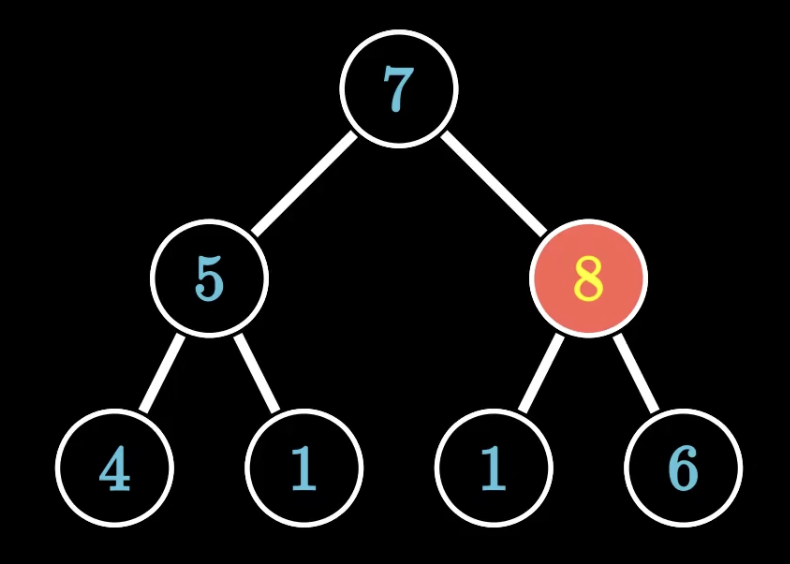
这颗完全二叉树下面的部分不符合大根堆的堆序性，该如何操作把树调整为堆呢？
image.png
我们拿这个节点与他的父节点做比较，如果大于则进行交换。
image.png
直到不再大于父节点或到达堆顶
image.png
这个操作主要用于插入新元素到堆中
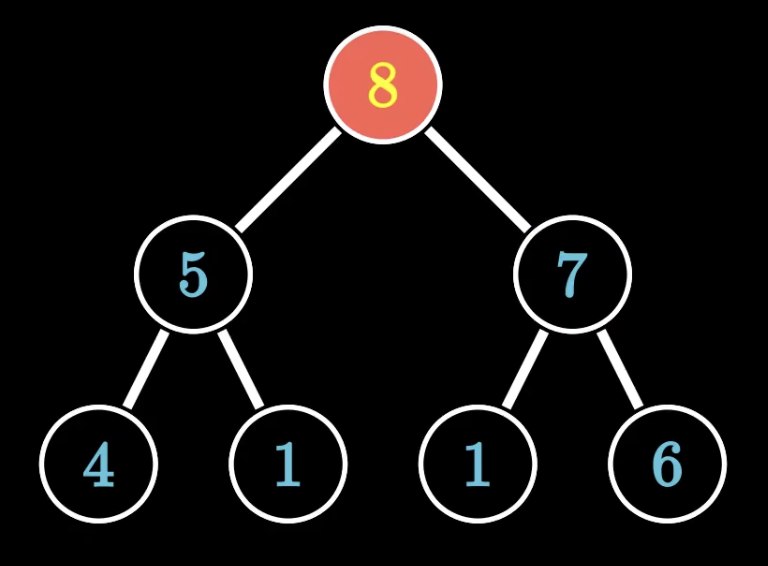
image.png

下滤

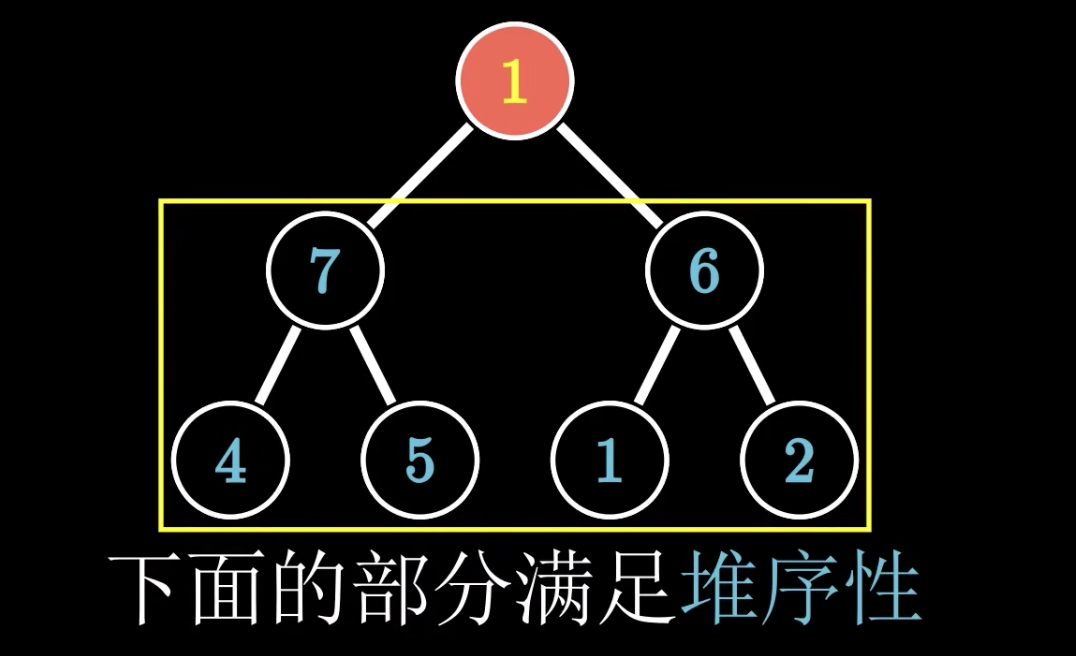
这颗完全二叉树下面的部分符合大根堆的堆序性，该如何操作把树调整为堆呢？
image.png
我们拿这个节点与他的最大子节点做比较，如果小于则进行交换。
image.png
持续比较，直到该元素大于它的子节点或者移动到底部为止！！！
image.png

堆的构造过程

自下而上建堆法

使用数组构建堆时，就是先按照层次将所有元素依次填入二叉树中，使其成为二叉树，然后再去不断调整，最终使其符合堆结构。
:::warning
这里先假设一个节点的下标为 i :
1、当 i = 0 时， 为根节点
2、当 i >= 1时，父节点为 (i - 1) / 2
size就是元素的个数，从1开始计数
:::
下面看如何建立一个大根堆：
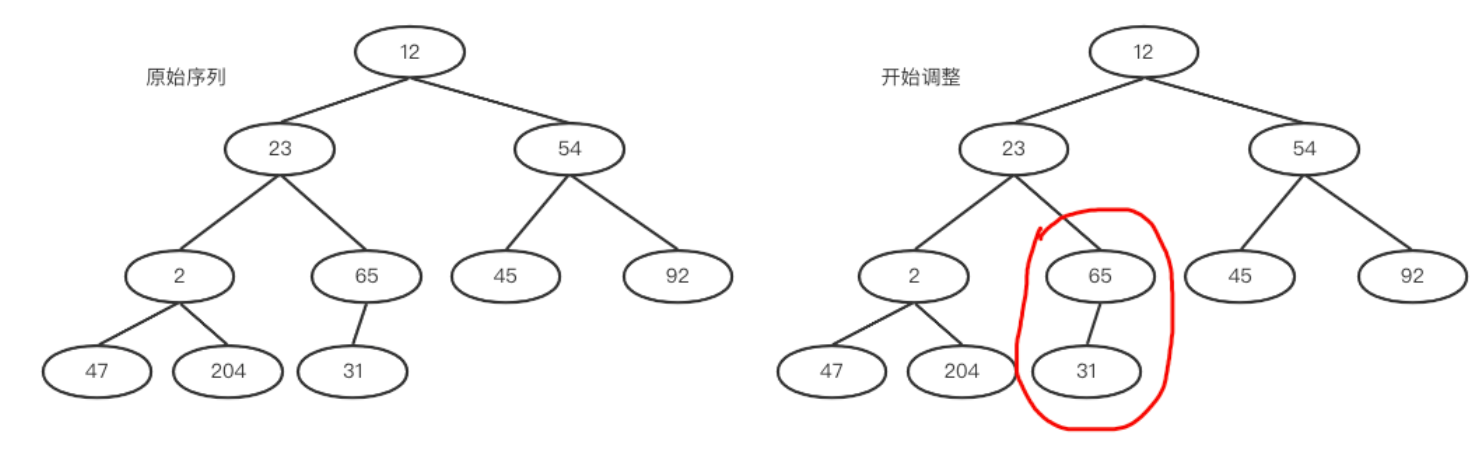
将元素依次排到完全二叉树节点上去，如下作图所示。
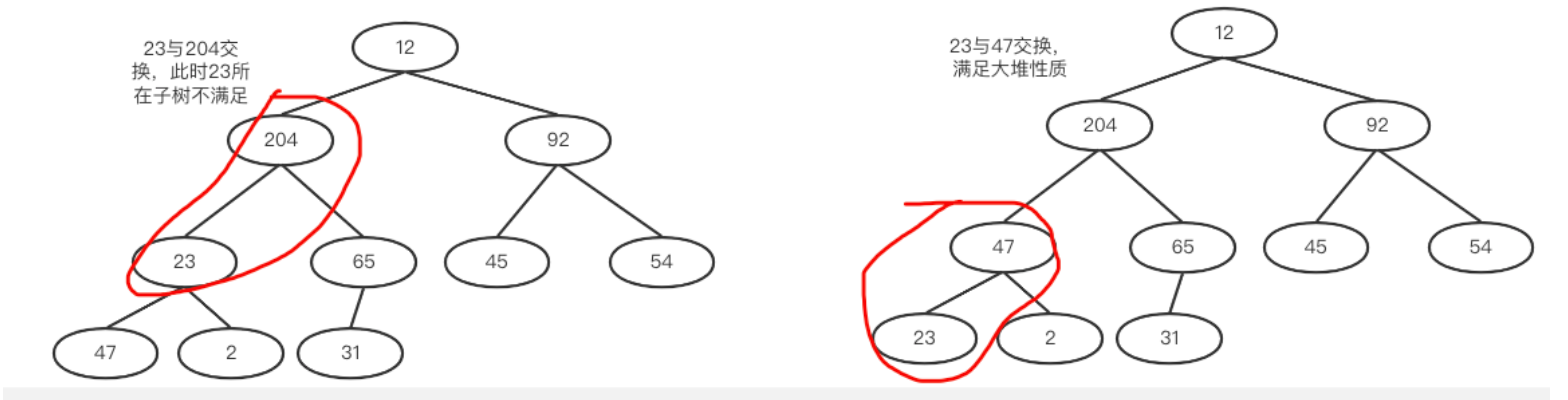
a. int i = (size - 2) / 2 = 4（思考一下为什么是 size - 2 而不是 size - 1)。找到数组中的4号下标（(10 - 2) / 2 = 4）。65大于其孩子，满足大堆性质，所以不用交换。如下右图

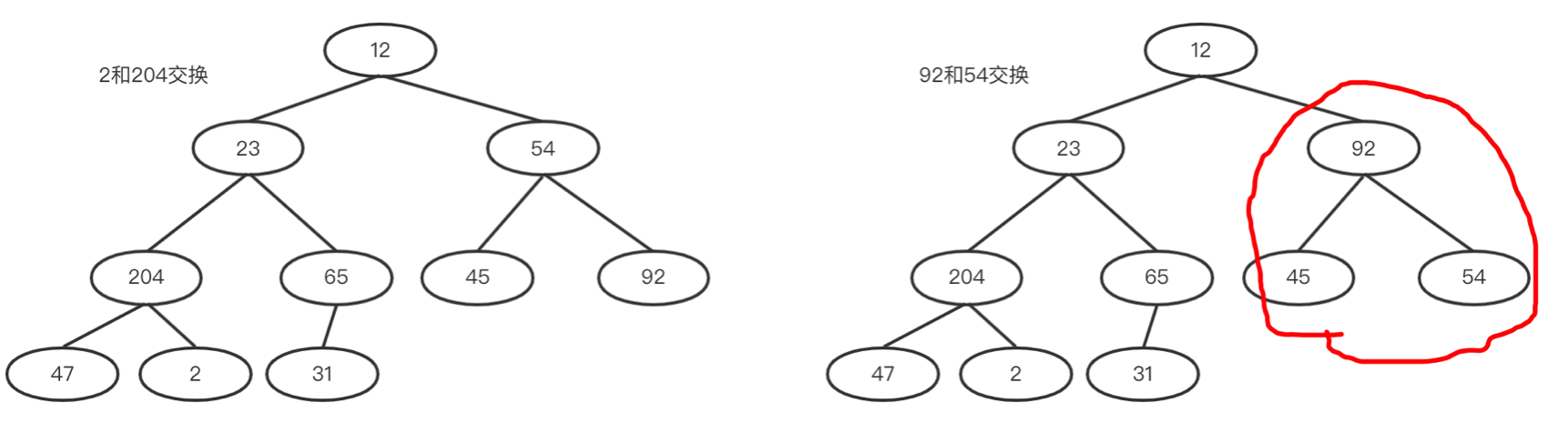
image.png

b. 然后 i = i - 1;用2和其最大的孩子进行比较，2和204交换。交换后204所在子树满足大堆，如下左图。
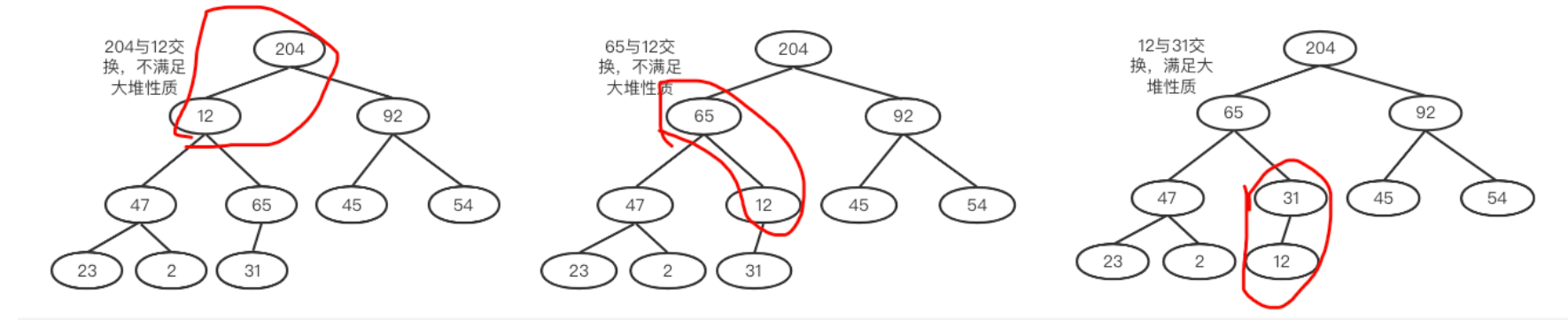
c. 继续i = i - 1;54和其最大的孩子进行比较，54和92交换。此时92所在子树满足大堆，如下右图。
image.png

d. 继续i = i - 1;23和其最大的孩子进行比较，23和204交换，交换结束后，23的子树此时不满足堆序性了，所以还需要调整它的子树。如下两图所示。
image.png

e. 继续i = i - 1;12和其最大的孩子进行比较，12和204进行交换，交换结束后，仍然出现不平衡的情况，以此类推，直到根节点也满足要求就完毕了。
image.png
这样我们就建好了一个大顶堆。
另外，对于同一组数据，如果输入的序列不一样，那最终构造的树是否也会不一样呢？非常有可能，那这样的树有什么意义呢？我们后面再看，这里先理解堆是这么构建的就行了。

插入操作

这里就会提到我们上面说的上滤啦！
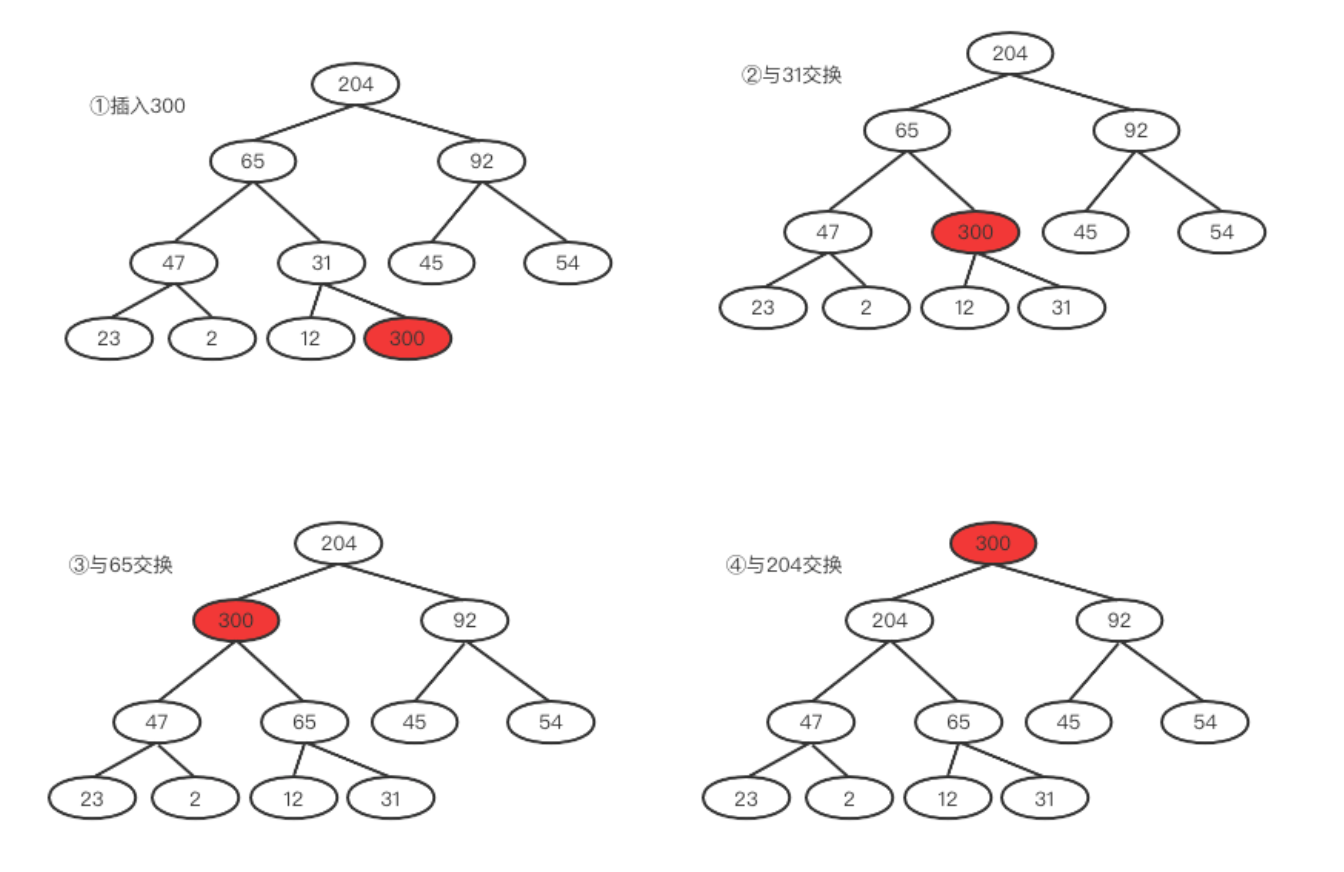
如果要插入一个新元素该怎么做呢？将元素插入到保持其为完全二叉树的最后一个位置，然后进行上滤。
每前进一层就要保证其子树都满足堆否则就去处理子树，直到完全满足要求。
看一个例子，如下图，我们插入一个300，我们将其插入到31的右孩子位置，然后不断向上爬，31 < 300，所以二者交换，再向上爬发现300大于65，二者交换。最后300大于根元素204，二者交换。最后得到了新的堆。
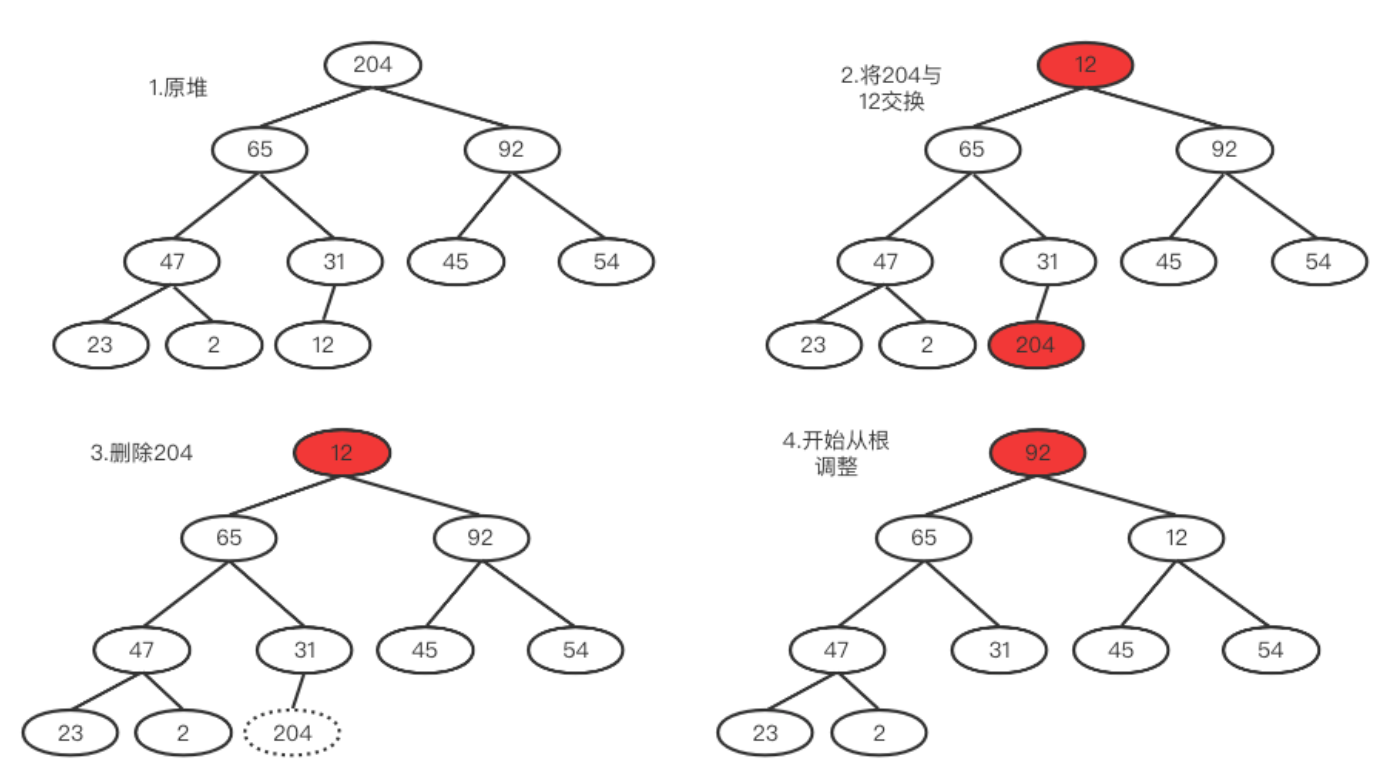
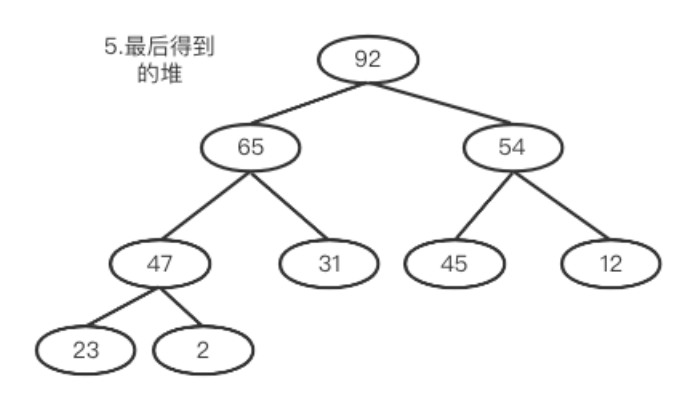
image.png

删除操作

堆本身比较特殊，一般对堆中的数据进行操作都是针对堆顶的元素，即每次都从堆中获得最大值或最小值，其他的不关心，所以我们删除的时候，也是删除堆顶。如果直接删掉堆顶，整个结构就被破坏了，群龙无首不易管理。所以实际策略是先将堆中最后一个元素(假如为A)和堆顶元素进行交换，然后删除堆中最后一个元素。这里就是下滤！！！之后再从根开始逐步与左右比较，谁更大谁上位。然后A再继续与子树比较，如果有更大的继续交换，知道自己所在子树满足大顶堆。
image.png
最后堆结构如下：
image.png

这个东西的价值在于大顶堆的根节点是整个树最大的那个，增加时会根据根的大小来决定要不要加，而删除操作只删除根元素。这个特征可以在很多场景下有奇妙的应用，后面的算法题全都基于这一点。

为什么堆的效率高呢？

因为堆元素的数量是有限制的，一般不用将所有的元素都放进堆里。后面题目中可以看到，在序列中找K大，则堆的大小就是K。如果K个链表合并，那么堆就是K。原理后面展开。
这么多堆的性质，我们看一下堆到底如何解决问题。关于堆的问题，记住口诀：

查找：找大用小，大的进；找小用大，小的进。
排序：升序用小，降序用大。

解释一下：是找K大，则用小顶堆，后续数据只有比根元素更大时才允许进入堆。如果是找K小，则对应反过来。后面我们结合例子分析为什么。